
A mathematical model is proposed to describe influence of stress on longevity in terms of organism protection. It was shown based on the general theory of mortality and aging (Strehler and Mildvan) and data on heating stress with C.elegans worms that an additional protection was initiated due to moderate (around one hour) duration of heating at sublethal (35oC) temperature applied at early stage of the worm life. The additional protection causes hormesis - increase in life expectancy after action of low dose of an negative agent.
Изучение реакции различных организмов и растений на стресс позволяет выявлять общие закономерности, лежащие в основе процессов развития, адаптации к изменяющимся внешним условиям, поддержания жизнедеятельности организмов и эволюционного процесса и процесса поддержании генетической стабильности вида [3,4,12,17]. При этом изучение влияния стресса на продолжительность жизни представляется наиболее перспективным, поскольку, с одной стороны, событие гибели легко поддаётся формализации и наблюдению, а с другой - продолжительность жизни служит биомаркером, отражающим сложные процессы старения, потери устойчивости и стабильности, протекающие в организме [9,10,16].
Особенный интерес вызывает экспериментально обнаруженное явления гормезиса [1], которое заключается в том, что малая доза вредного агента может привести к позитивному эффекту, например, к увеличению всхожести семян после радиационного облучения [14], повышению выживаемости червей при рентгеновском облучении после оксидативного стресса [20], увеличение продолжительности жизни и термической устойчивости крыс при ограничении питания [7]. При анализе причин повышения сопротивляемости и выживаемости организмов под действием стресса выделяют три основных механизма: снижение метаболизма, и, соответственно, выделения вредоносных веществ [15]; активация продукции антиоксидантов, защищающих организм от действия свободных радикалов, образующихся в процессе жизнедеятельности и влияния внешней среды [11]; активация продукции белков теплового шока - heat shok proteins, появляющихся в результате любого стресса и также защищающих организм [5, 6]. Формально, все эти механизмы можно рассматривать как единую систему, защищающую организм от гибели. Её действие удобно рассмотреть в терминах вероятности гибели, используя опыт моделирования процессов дожития.
Математическая модель
Рассмотрим стохастический процесс сохранения жизнедеятельности организма в условиях негативного воздействия на него со стороны окружающей и внутренней среды. В теоретико-вероятностных терминах конкретные воздействия на организм составляют пространство элементарных событий
а множество воздействий на организм, при которых он сохраняет свои
функциональные способности в течении времени ![]() ,
образует событие
,
образует событие ![]() дожития до возраста
дожития до возраста ![]() .
Ясно, что с ростом
.
Ясно, что с ростом ![]() события
события ![]() образуют систему вложенных множеств, а вероятностная мера этих множеств
задает невозрастающую функцию дожития до возраста
образуют систему вложенных множеств, а вероятностная мера этих множеств
задает невозрастающую функцию дожития до возраста ![]()
![]() ,
имеющую смысл вероятности дожития до возраста
,
имеющую смысл вероятности дожития до возраста ![]() .
Конкретный вид функции дожития определяется вероятностными свойствами процесса
разрушения организма и может быть описан математически при ряде допущений.
.
Конкретный вид функции дожития определяется вероятностными свойствами процесса
разрушения организма и может быть описан математически при ряде допущений.
Одним из возможных подходов к описанию вероятностного процесса потери организмом своих функциональных возможностей является теория старения, предложенная Стреллером и Милдваном и основанная на концепции витальности - характеристики, отражающей внутреннюю способность организма сохранять жизнедеятельность при негативных воздействиях. Уровень негативных воздействий отражает как внешние условия существования организма, так и состояние его защитных и репарационных механизмов, которые не отражены в витальности. Чем хуже условия существования организма, тем выше этот уровень. Чем лучше организм защищен и чем эффективнее работают системы его восстановления - тем ниже эффективный уровень негативных воздействий. Условием наступления смерти является превышение негативным воздействием уровня витальности в конкретном возрасте. При допущениях, что витальность линейно снижается с возрастом а негативные воздействия имеют случайный характер и распределены по закону Больцмана, в [18] показано, что вероятность дожития до возраста x описывается соотношением, называемым законом Гомперца,
| (1) |
Рассмотрим подробнее влияние защитных систем организма на вероятность
дожития до возраста ![]() .
Допустим, что в организме существуют две взаимно дополняющие системы защиты
от негативных воздействий. Событие
.
Допустим, что в организме существуют две взаимно дополняющие системы защиты
от негативных воздействий. Событие ![]() соответствует дожитию до возраста
соответствует дожитию до возраста ![]() при наличии только первой защиты, событие
при наличии только первой защиты, событие ![]() соответствует дожитию до возраста
соответствует дожитию до возраста ![]() при наличии только второй защиты. Вероятность дожития до возраста
при наличии только второй защиты. Вероятность дожития до возраста ![]() при действии обеих защит вычисляется как
при действии обеих защит вычисляется как
Обе защиты предохраняют организм от одних и тех же воздействий, что
означает, что события ![]() и
и ![]() вложены и
вложены и
| (2) |
Результаты моделирования
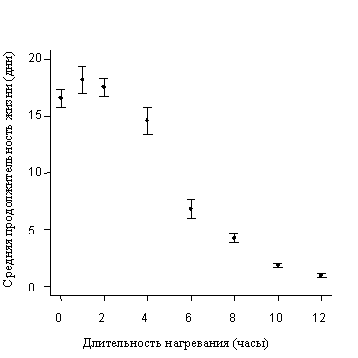 |
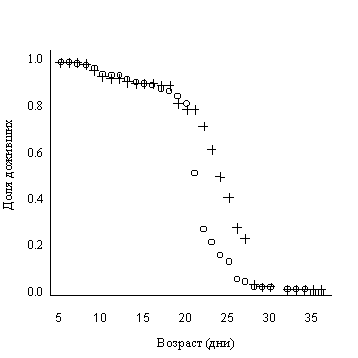 |
Изучение доли червей, доживших до определённого возраста в контрольной группе показало, что на интервале 5-19 дней эта кривая хорошо описывается с помощью кривой дожития Гомперца. В рамках теории Стреллера - Миддвана из этого следует, что на возрастном интервале 5-19 дней действует постоянная, независящая от возраста защита, универсальная для всех членов популяции. Резкое падение доли живых червей после 19 дней жизни означает резкое изменение защитных сил организма - переход в новое состояние. Расчеты показали, что кривая дожития червей для возрастов старше 19 дней хорошо описывается кривой дожития, наблюдаемой в неоднородной популяции, имеющей более слабую защиту [13]. Результирующая модельная кривая, имитирующая наличие двух состояний защиты приведена на рис 3.
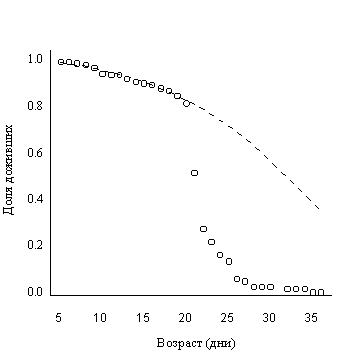 |
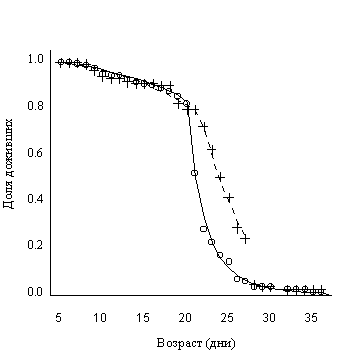 |
Наличие двух состояний защиты, обнаруженное путем моделирования данных о дожитии червей, представляет самостоятельный интерес. На наличие двух фаз в кривой смертности C.elegans указывается описано в литературе [8,19], в [13] отмечена связь этих фаз с уровнями функционирования систем поддержания жизни. В [21] подчеркивается универсальность концепции наличия дискретных состояний на уровне клетки и организма.
Переключение между состояниями защиты можно описать в рамках качественной
теории нестационарных динамических моделей. Пусть для поддержания жизнедеятельности
организма в возрасте ![]() требуется в среднем количество энергии
требуется в среднем количество энергии ![]() Организм гибнет если случайный выброс энергетической потребности организма
превысит детерминированный уровень
Организм гибнет если случайный выброс энергетической потребности организма
превысит детерминированный уровень ![]() - уровень витальности. Среднее количество энергии
- уровень витальности. Среднее количество энергии ![]() определяется как внешними условиями (температура, питание), так и наличием
у организма средств специализированной и универсальной защиты (антиоксиданты,
специализированные белки и т.д.). Будем считать, что
определяется как внешними условиями (температура, питание), так и наличием
у организма средств специализированной и универсальной защиты (антиоксиданты,
специализированные белки и т.д.). Будем считать, что ![]() пропорционально уровню вредных веществ
пропорционально уровню вредных веществ ![]() ,
вырабатываемых в процессе жизнедеятельности организма. В условиях постоянной
внешней среды этот уровень регулируется экспрессией и темпом расхода защитных
веществ организма, уровень которых обозначим
,
вырабатываемых в процессе жизнедеятельности организма. В условиях постоянной
внешней среды этот уровень регулируется экспрессией и темпом расхода защитных
веществ организма, уровень которых обозначим ![]() .
Предполагая, что в масштабе времени, характерном для изменения процессов
.
Предполагая, что в масштабе времени, характерном для изменения процессов ![]() и
и ![]() ,
параметры организма не изменяются, динамику изменения уровня вредных и
защитных веществ можно описать системой дифференциальных уравнений
,
параметры организма не изменяются, динамику изменения уровня вредных и
защитных веществ можно описать системой дифференциальных уравнений
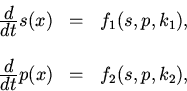
где ![]() и
и ![]() - параметры, изменяющиеся существенно медленнее процессов
- параметры, изменяющиеся существенно медленнее процессов ![]() и
и ![]() .
Характерный для задач метаболического контроля [2] вид кривых
.
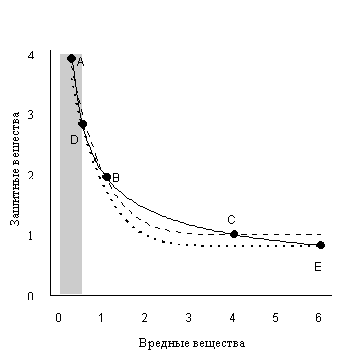
Характерный для задач метаболического контроля [2] вид кривых![]() и
и ![]() на фазовой плоскости в условном масштабе приведен на рис. 5.
на фазовой плоскости в условном масштабе приведен на рис. 5.
 |
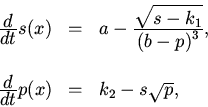
причем параметры ![]() и
и ![]() имеют смысл темпа экспрессии и минимально возможного уровня защитных веществ
в организме, а параметры
имеют смысл темпа экспрессии и минимально возможного уровня защитных веществ
в организме, а параметры ![]() и
и ![]() характеризует темп образования и максимально допустимый уровень вредных
веществ.
характеризует темп образования и максимально допустимый уровень вредных
веществ.
Точки пересечения кривых A, B и C соответствуют стационарным значениям уровней защитных и вредных веществ. При этом нетрудно видеть, что точки A и C соответствуют устойчивым по отношению к колебаниям уровня вредных веществ стационарным точкам, а точка B - неустойчивой. В начале жизни организм содержит малое количество вредных веществ, находится в окрестности точки A, и за короткое время попадает в устойчивое стационарное состояние A. Поскольку темп образования вредных веществ подвержен случайным флуктуациям, содержание их в организме колеблется в пределах заштрихованной на рис. 5 области возле устойчивого состояния.
По мере старения организма параметр ![]() - минимально возможный уровень защитных веществ в организме, уменьшается,
что ведёт к перемещению неустойчивой точки B в положение D ближе к точке
A. Это перемещение продолжается до тех пор, пока точка неустойчивого равновесия
D не попадет в заштрихованную область, после чего организм переходит в
новое устойчивое состояние E с высоким уровнем вредных веществ. Время этого
переходного процесса мало, что позволяет говорить о скачкообразном переключении
защиты.
- минимально возможный уровень защитных веществ в организме, уменьшается,
что ведёт к перемещению неустойчивой точки B в положение D ближе к точке
A. Это перемещение продолжается до тех пор, пока точка неустойчивого равновесия
D не попадет в заштрихованную область, после чего организм переходит в
новое устойчивое состояние E с высоким уровнем вредных веществ. Время этого
переходного процесса мало, что позволяет говорить о скачкообразном переключении
защиты.
Выводы
Проведенные расчеты показывают, что наблюдаемый эффект увеличения средней продолжительности жизни может быть объяснен активацией специфической защиты в результате нагревания. В группе червей, подвергшейся нагреванию в течении одного часа, до возраста 20 дней эта специфическая защита оказывается менее эффективной, чем генетически обусловленная защита. В соответствии с (2) вероятность дожития на этом возрастном интервале определяется дожитием в контрольной группе. После 20 дней жизни генетически обусловленная защита становится менее эффективной, чем активированная специфическая защита. и вероятность дожития определяется этой защитой. Действие специфической защиты заканчивается в возрасте 28 дней после чего вероятности дожития в контрольной группе и группе, подвергнувшейся нагреванию в течение одного часа, совпадают. Как генетически обусловленная, так и активированная стрессом защита обладают двумя устойчивыми состояниями, переходы между которыми осуществляются скачкообразно вследствие медленного изменения параметров организма с возрастом.
Сделанные выводы о механизме возникновения гормезиса могут быть проверены экспериментально путем изучения изменений, вызванных стрессовыми нагрузками, в возрастной зависимости биохимических показателей червей.
 Ваши комментарии
Ваши комментарии
|
![[SBRAS]](s_sigma.gif)
[Головная страница] [Конференции] [СО РАН] |
© 2001, Сибирское отделение Российской академии наук,
Новосибирск
© 2001, Объединенный институт информатики СО РАН, Новосибирск
© 2001, Институт вычислительных технологий СО РАН, Новосибирск
© 2001, Институт систем информатики СО РАН, Новосибирск
© 2001, Институт математики СО РАН, Новосибирск
© 2001, Институт цитологии и генетики СО РАН, Новосибирск
© 2001, Институт вычислительной математики и математической
геофизики СО РАН, Новосибирск
© 2001, Новосибирский государственный университет
Дата последней модификации Saturday, 08-Sep-2001 17:38:20
NOVST